Dans un article précédent, nous avons présenté les particularités d’un phénomène connu sous le nom de coup de bélier qui se produit dans les réseaux hydrauliques en général, et dans ceux des parcs aquatiques en particulier. Dans cette nouvelle étude du même phénomène, nous distinguerons le coup de bélier rapide du coup de bélier lent, en fonction du temps de fermeture de la vanne d’arrêt, et nous présenterons différentes formulations pour calculer la surpression associée à chacun de ces types de coup de bélier. Enfin, nous présenterons les cas spécifiques dans lesquels le coup de bélier se produit dans les installations hydrauliques des parcs aquatiques, ainsi que les mesures disponibles pour l’atténuer.
Dans le cadre du même exemple utilisé dans l’article précédent, nous déterminons que le temps de fermeture (Tc) correspond à la durée de la manœuvre de coupure du débit dans la conduite. De même, le temps nécessaire à l’onde de surpression (de vitesse a) pour parcourir la conduite (de longueur L), de la vanne d’arrêt (CV) au réservoir (T), nous l’appellerons L/a. Par conséquent, l’onde réfléchie par le réservoir atteindra la vanne en 2·L/a.
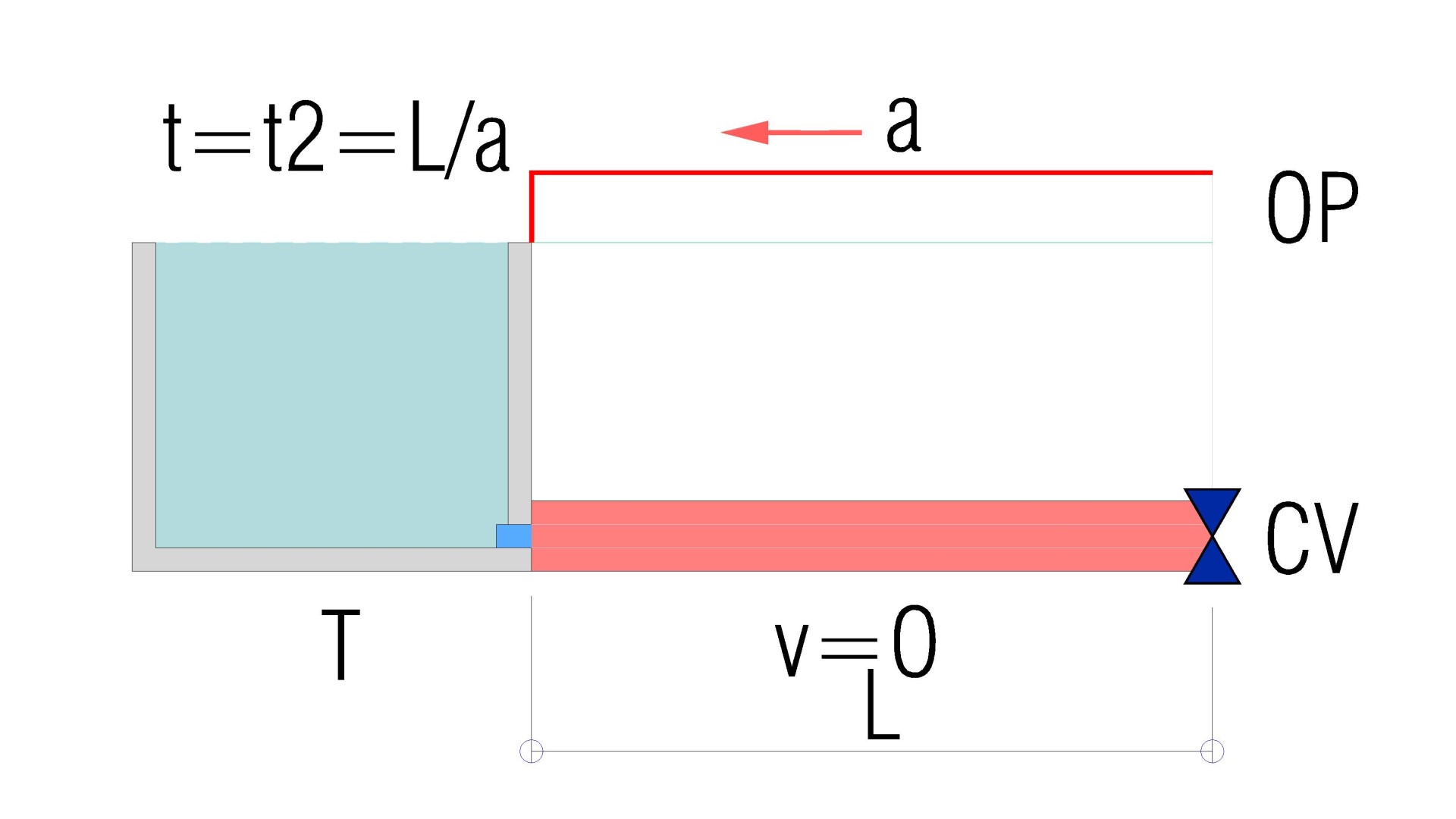
L’image montre l’instant t2 = L/a, lorsque l’onde de surpression atteint le réservoir.
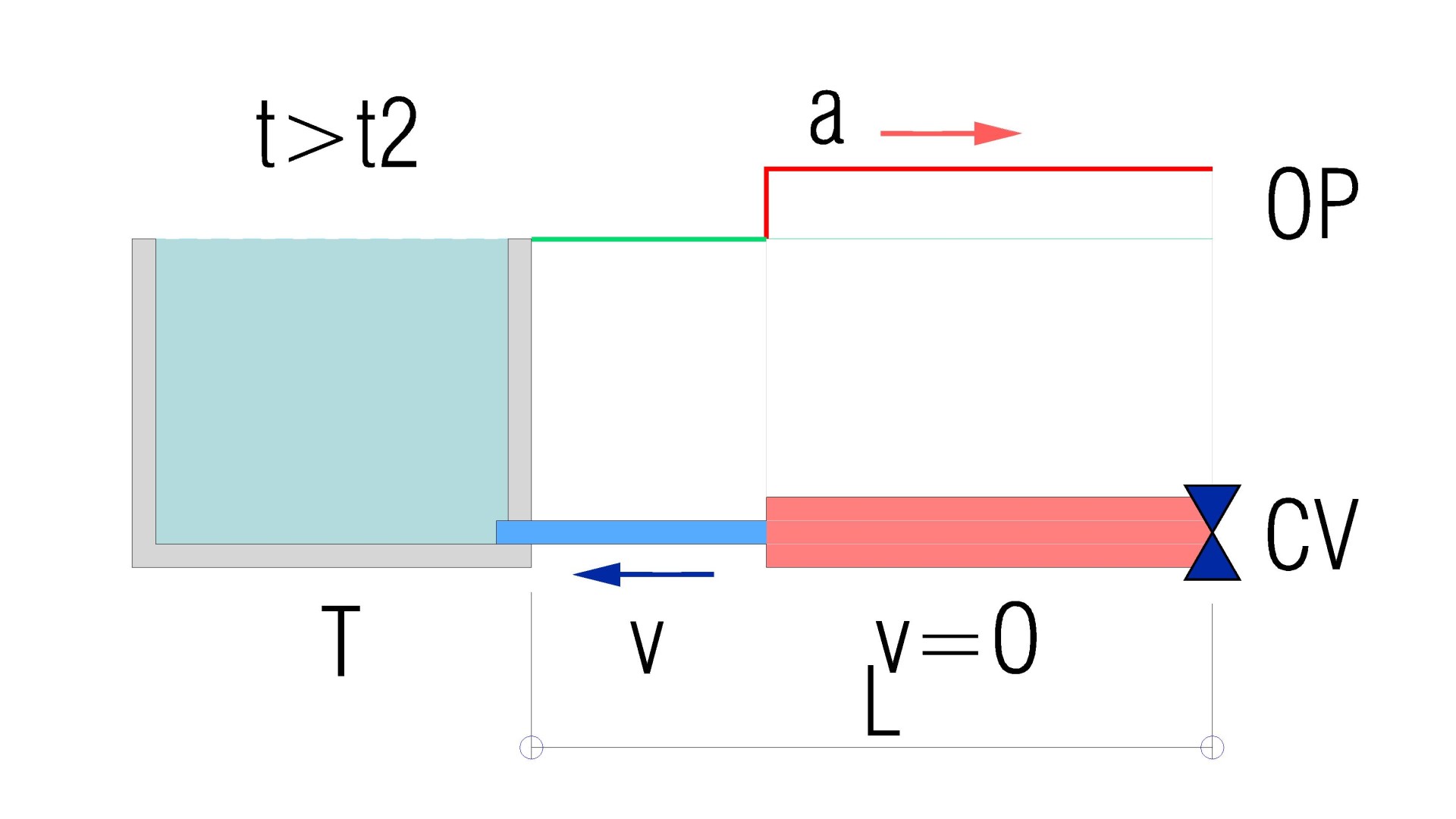
L’onde de pression est ensuite réfléchie vers la vanne d’arrêt.
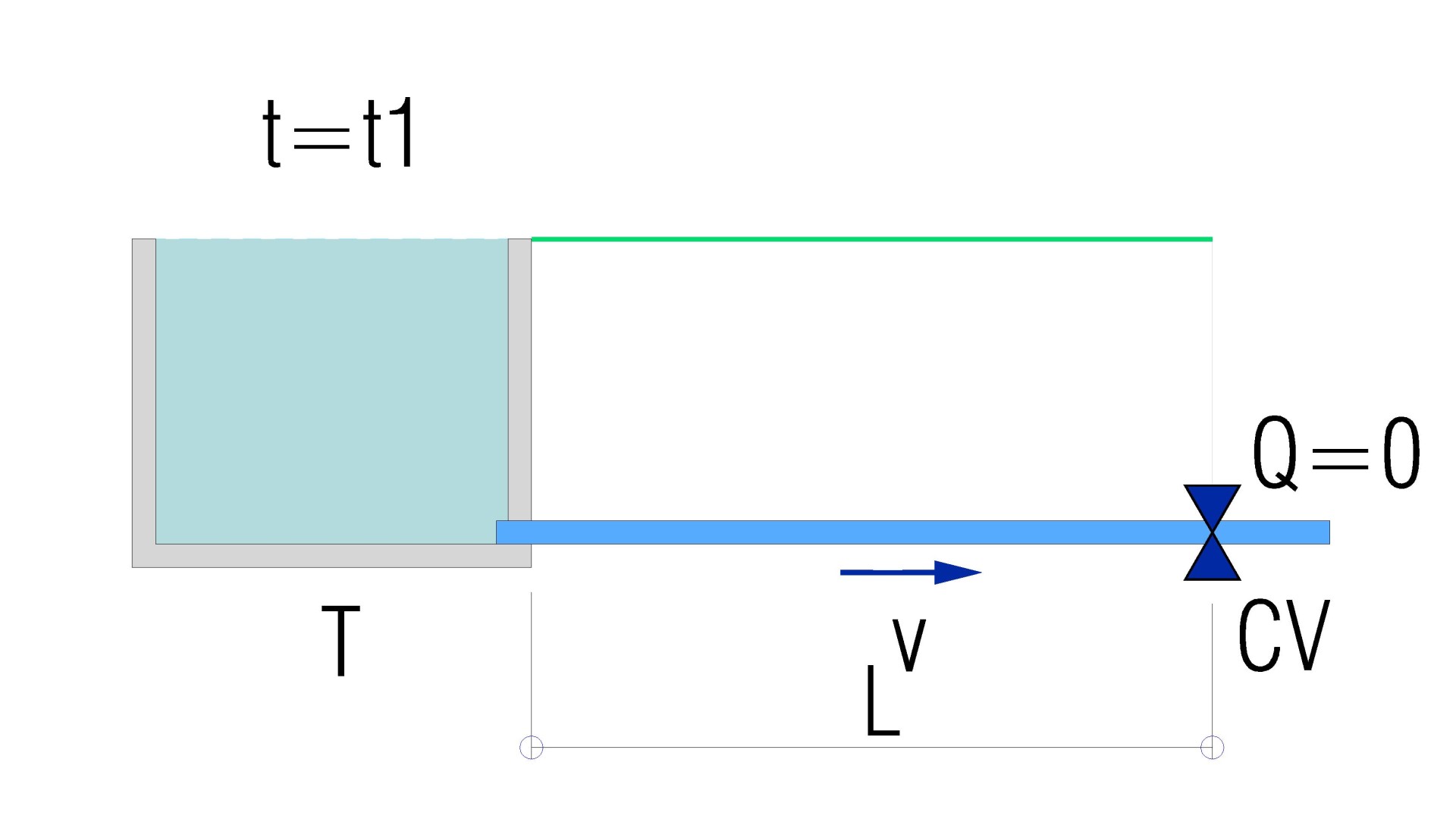
C’est donc à l’instant t3 = 2·L/a, que l’onde de pression atteint la vanne d’arrêt.
Lorsque la fermeture est rapide ou, en d’autres termes, Tc < 2·L/a, l’onde de surpression atteint la vanne alors qu’elle est déjà complètement fermée. Dans ce cas, la surpression (OP) est calculée avec la formule d’Allievi, comme suit :
OP = a·v/g
où :
a : vitesse de l’onde
v : vitesse du fluide
g : accélération de la gravité
Ainsi, en cas de fermeture rapide, la surpression est indépendante du temps de fermeture, et est équivalente à celle qui se produirait si la fermeture était instantanée, ou Tc ≈ 0.
Lorsque la fermeture est lente, ou Tc > 2·L/a : dans ce cas, l’onde de surpression atteint la vanne alors qu’elle n’est pas encore complètement fermée, ce qui signifie qu’une partie de la surpression est déchargée. Dans cette situation, la surpression est calculée à l’aide de la formule de Michaud :
OP = 2·L·v/(g·Tc)
Comme on peut le voir, en cas de fermeture lente, la surpression est inversement proportionnelle au temps de fermeture de la vanne. Ainsi, plus le temps de fermeture est long, plus faible est la surpression dans la conduite due au coup de bélier.

Les installations hydrauliques des parcs aquatiques, avec de grandes unités de pompage à partir desquelles l’eau est pompée vers les toboggans et autres attractions, peuvent être soumises à des coups de bélier lors de la manœuvre d’arrêt de la pompe. Dans ce cas, un front d’onde de pression négative est produit et, par conséquent, un coup de bélier est déclenché dans sa phase inverse. Pour atténuer cet effet, il faut s’assurer que le temps d’arrêt de la pompe (équivalent au temps de fermeture de la vanne, ou Tc, décrit ci-dessus) est plus long que le temps de déplacement de l’onde de pression 2·L/a. Nous serons donc dans l’option de fermeture lente (arrêt lent de la pompe) et, par conséquent, la surpression produite dans la conduite sera ostensiblement plus faible. Il va de soi que plus l’arrêt est lent, plus la surpression sera faible.
En pratique, afin d’éviter les coups de bélier, les pompes des parcs aquatiques sont souvent équipées de convertisseurs de fréquence ou de démarreurs progressifs. Ces dispositifs garantissent que les pompes s’arrêtent suffisamment lentement pour que la surpression produite dans la canalisation soit négligeable.
Par Luis Llor, ingénieur hydraulique senior au sein du département d’architecture d’Amusement Logic.