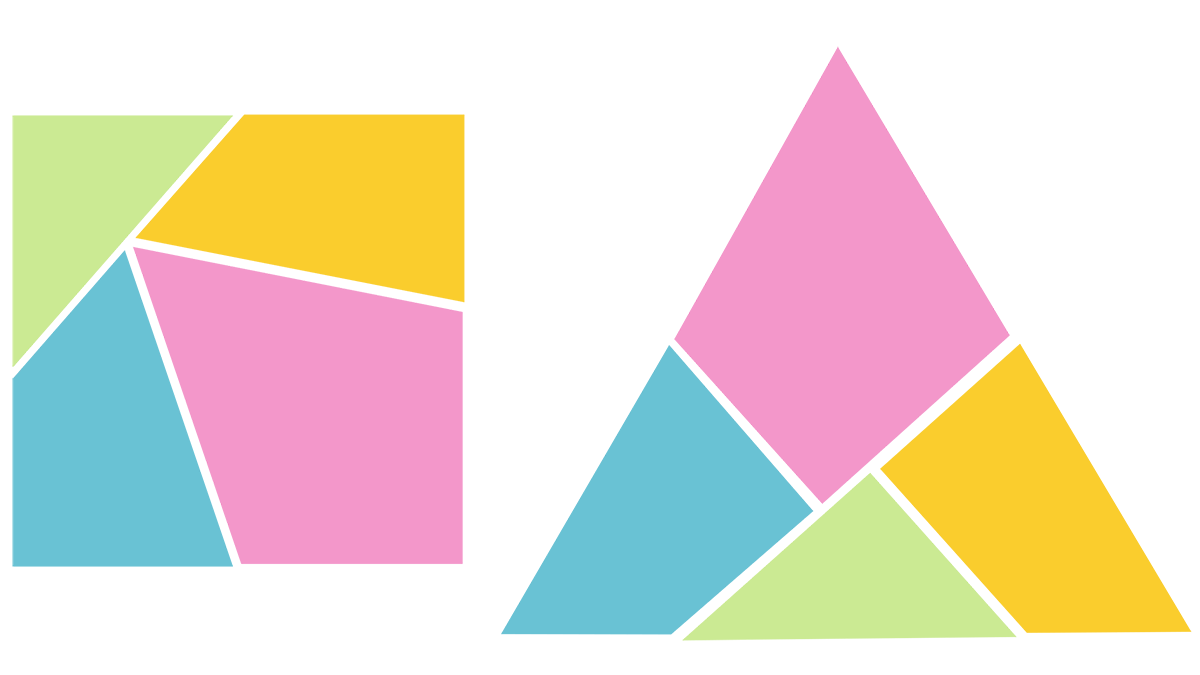En 1902, le mathématicien anglais Henry Ernest Dudeney (1857-1930) proposait dans sa rubrique de jeux mathématiques, publiée dans le supplément dominical Weekly Dispatch — connu ensuite sous le nom de Sunday Dispatch de 1928 à 1961, année où il fusionna avec le Sunday Express — un défi en apparence simple mais d’une complexité fascinante : comment découper un triangle équilatéral en un nombre minimal de pièces, de sorte qu’en les réassemblant (uniquement par translation et rotation, sans superposition), on obtienne un carré parfait ?
Un lecteur nommé Charles William McElroy proposa une solution ingénieuse : quatre pièces reliées par leurs sommets et articulées, formant une sorte de puzzle mécanique permettant, par une simple rotation, de transformer le triangle en carré. Pendant 122 ans, personne n’a réussi à trouver une solution avec moins de quatre pièces, bien qu’aucune preuve formelle n’en ait jamais confirmé l’impossibilité.
Ces doutes furent levés en décembre 2024, lorsque les mathématiciens Tonan Kamata et Ryuhei Uehara, de l’Institut Avancé de Science et Technologie du Japon, ainsi que Erik D. Demaine du Massachusetts Institute of Technology (MIT), démontrèrent qu’il est mathématiquement impossible de résoudre ce problème avec moins de quatre pièces. Ainsi, la solution de McElroy et Dudeney, proposée il y a plus d’un siècle, est bel et bien optimale — autrement dit, aucune solution plus efficace n’existe.
Pour résoudre l’énigme géométrique, Kamata et ses collègues l’ont réduite à un problème de théorie des graphes. Plutôt que de tester un nombre infini de découpes géométriques, ils ont représenté chaque découpe comme une arête, et chaque point d’intersection comme un sommet. Cette modélisation leur a permis de classer toutes les variantes possibles en catégories finies et gérables, transformant ainsi un problème infini en un ensemble fini de cas à examiner. Le résultat, vous le connaissez désormais.
Au-delà de sa valeur théorique, cette découverte a des implications pratiques dans des domaines variés tels que le design, l’architecture ou encore la pédagogie mathématique. À titre d’exemple, le studio de design et d’architecture londonien DHaus a transposé le puzzle de Dudeney — également connu sous le nom de «dissection de Dudeney» ou «problème du mercier» (en référence à l’énigme n° 26 du recueil The Canterbury Puzzles, publié en 1907, où un mercier propose à ses interlocuteurs de découper un triangle équilatéral de tissu pour en faire un carré parfait) — en table et même en maison aux parties mobiles.
Comme vous le voyez, des problèmes en apparence simples peuvent receler des profondeurs insoupçonnées. Quoi qu’il en soit, la prochaine fois que vous croiserez un triangle ou un carré, souvenez-vous qu’au-delà de leur apparente immobilité se cachent parfois des connexions inattendues, des transformations étonnantes, et surtout, l’élégance éternelle des mathématiques.
Sources: Arxiv.org, Scientific American, Wolfram MathWorld, Gutenberg.org, Wikipedia.
Images: DHaus 1, DHaus 2, Wikipedia.